Activate or Not: Learning Customized Activation

Ma, Ningning, et al. "Activate or Not: Learning Customized Activation."
Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2021.

먼저 알면 좋은 것들

Swish Activation Function ^[1]

$$\operatorname{swish}(x):=x \times \sigma(\beta x)=\frac{x}{1+e^{-\beta x}}$$

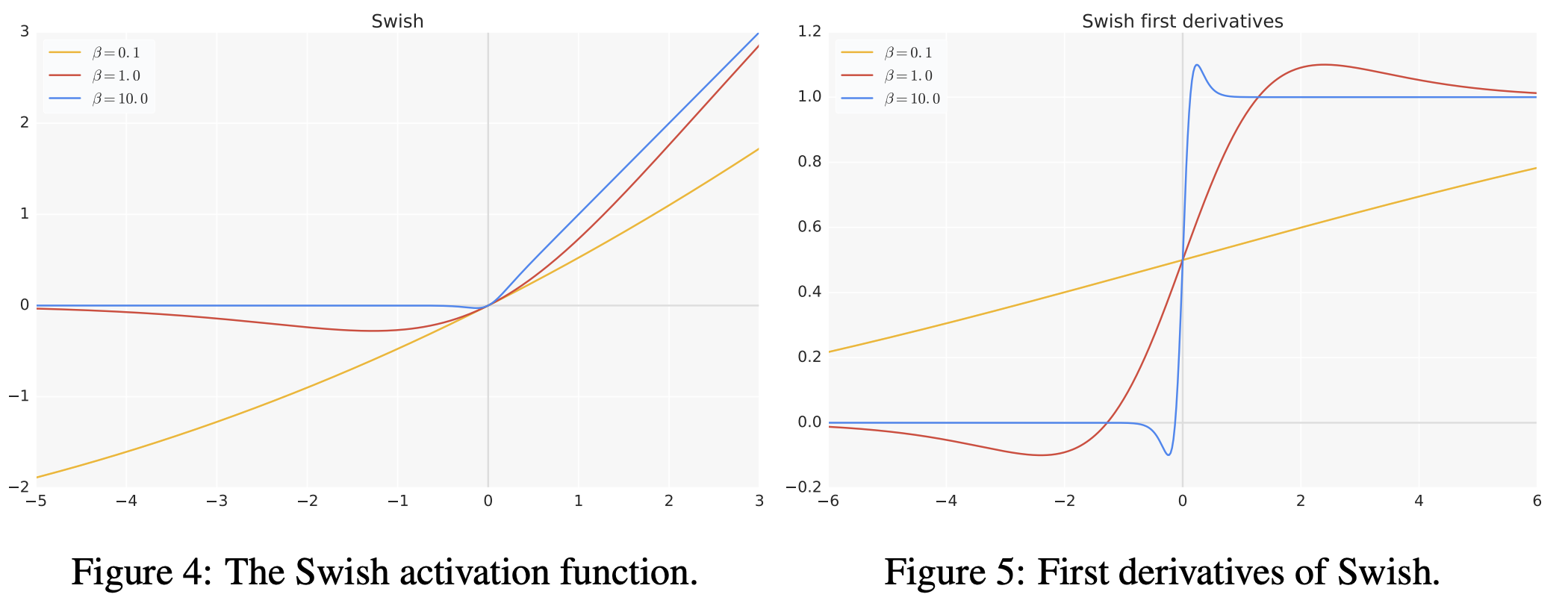
• Linear Function과 ReLU 사이에서의 non-linearly interpolated activation을 보여줍니다.
  • $β = 0$ 일 경우, Linear function $f(x) = x/2$ 처럼 작용하게 됩니다.
  • 반대로 $β → ∞$일 경우, Sigmoid에 해당하는 부분이 0-1 activation처럼 작용하게 되어, Swish가 ReLU처럼 작용하게 됩니다.
  • $β = 1$일 경우, 강화학습에서 사용되는 Sigmoid-weighted Linear Unit (SiL) function처럼 작용할 수 있습니다.
  • $β$는 위에서 보신 것처럼 어떤 상수일 수도 있고, 모델에 따라서는 훈련 가능한 파라미터가 될 수도 있습니다.
• 브레인팀 AI Scientist분들이 자주 사용하시는 Activation Function이기도 하죠 🙂
• Generative Model에서도 ReLU 대신 사용하는 경우가 많이 있습니다.
• 최근에는 Implicit Representation Network 상에서도 Swish가 다시금 주목을 받고 있습니다.
  • SIREN에서 언급하는 periodic function activation (Sine 함수 등) 보다 Swish가 더 나은 성능을 보이는 Task가 있습니다.

Sigmoid

$$\sigma(x)=\frac{1}{1+e^{-x}}$$

• 여기서는 Activation으로 시사하기보다는 수식 표현 시에 sigmoid로 묶어 표현하기 위해 확인하고 넘어가야 합니다.
• Swish가 결국 input 값에 sigmoid한 것과 input 값의 곱으로 표현된다(β 를 곱하기는 하겠지만)는 것도 다시 한번 리마인드하고 넘어갑시다 😎

Maxout Family

• ReLU와 같은 Activation Function의 출발점에 해당하는 개념 중 하나입니다.
• Goodfellow와 Bengio의 논문^[2] 으로, Maximum을 선택하는 것으로도 임의의 Convex Function에 대해 두루 근사할 수 있음을 시사합니다.

Main Idea

ACON(ActivationOrNot) Activation Function

$$\operatorname{ACON-C}(x) := \left(p_{1}-p_{2}\right) x \cdot \sigma\left(\beta\left(p_{1}-p_{2}\right) x\right)+p_{2} x$$

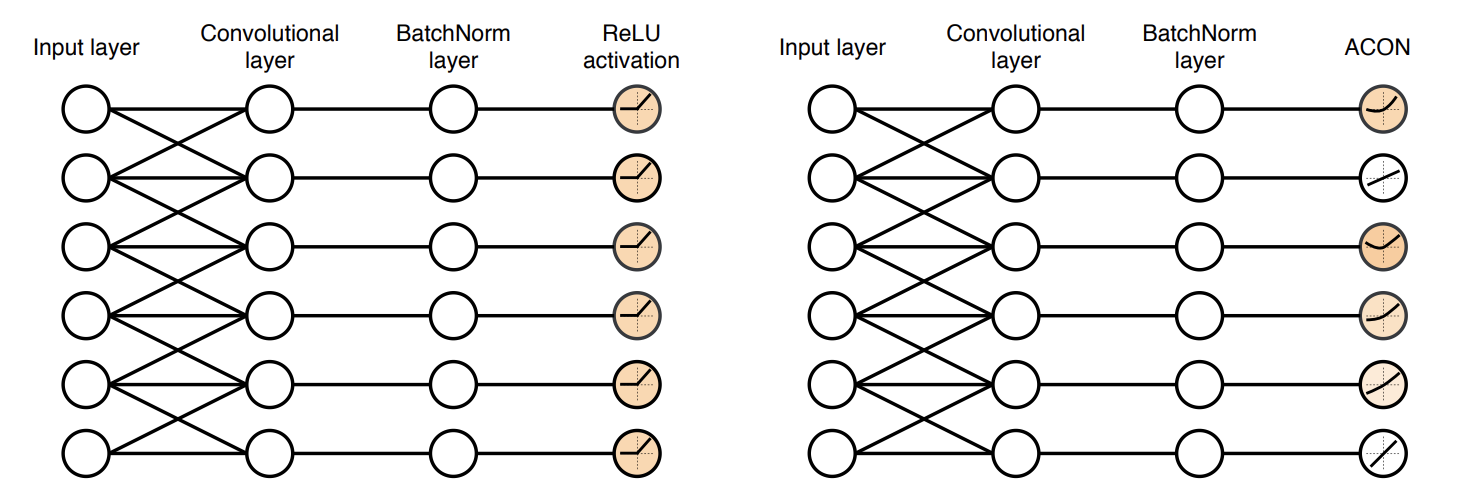
ACON Activation을 사용하였을 때, 특정 Layer의 Activation이 Linear 하게 pass수도, Non-linear Activation으로 활성될 수도 있습니다

저자는 ACON(더 나아가서 Meta-ACON)이라고 하는 Activation Function을 제안합니다. ACON activation은 trainable한 activation으로 Neuron을 Activation할 지 안 할지를 각 Layer의 특성에 맞게 결정합니다.

어떻게 해서 ACON 식을 도출할 수 있게 되었을까요?

먼저 Maximum Function $max(x1, ..., xn)$ 에 대해 smooth된 버전을 보아야 합니다. Maximum을 구한다는 것은 일반적으로 differentiable하지 않지만, 이를 smooth한 함수는 differentiable하게 됩니다.

보통 아래의 식처럼 표현합니다.

$$S_{\beta}\left(x_{1}, \ldots, x_{n}\right)=\frac{\sum_{i=1}^{n} x_{i} e^{\beta x_{i}}}{\sum_{i=1}^{n} e^{\beta x_{i}}}$$

이 때, $β$ 는 switching factor로서

• $β → ∞$일 때, 주어진 함수는 Maximum Function 의 역할을 하게 됩니다.
• $β → 0$일 때, 주어진 함수는 산술평균(Arithmetic Mean, 우리가 일반적으로 아는 평균)처럼 작동합니다.

일반적으로 Neural Network에서 많이 사용하는 Activation Function들은 위에서 언급한 Maxout에 준하는 것으로 표현할 수 있습니다.

$$max( ηa(x), ηb(x))$$

예를 들어, ReLU는 $ηa(x)=x$, $ηb(x)=0$인 것으로 생각하면, 이 역시 Maxout Family에 속한다고 볼 수 있습니다.
Leaky ReLU, FReLU 등도 이러한 방식으로 접근해보면 모두 Maxout Family에 속하게 됩니다.

본 논문에서의 목표는 Maximum Function과 위 Maxout Family를 함께 사용하여, Maxout Family 각각에 상응하는 activation function들을 smooth한 함수로 근사해보는 것입니다. 위에서 Smooth된 Maximum Function을 작성할 때, 입력 값의 개수를 2개로만 한정해서 식을 전개하면 딱이겠네요!

$$\begin{array}{l}S_{\beta}\left(\eta_{a}(x), \eta_{b}(x)\right) \\=\eta_{a}(x) \cdot \frac{e^{\beta \eta_{a}(x)}}{e^{\beta \eta_{a}(x)}+e^{\beta \eta_{b}(x)}}+\eta_{b}(x) \cdot \frac{e^{\beta \eta_{b}(x)}}{e^{\beta \eta_{a}(x)}+e^{\beta \eta_{b}(x)}} \\=\eta_{a}(x) \cdot \frac{1}{1+e^{-\beta\left(\eta_{a}(x)-\eta_{b}(x)\right)}}+\eta_{b}(x) \cdot \frac{1}{1+e^{-\beta\left(\eta_{b}(x)-\eta_{a}(x)\right)}} \\=\eta_{a}(x) \cdot \sigma\left[\beta\left(\eta_{a}(x)-\eta_{b}(x)\right)\right]+\eta_{b}(x) \cdot \sigma\left[\beta\left(\eta_{b}(x)-\eta_{a}(x)\right)\right] \\=\left(\eta_{a}(x)-\eta_{b}(x)\right) \cdot \sigma\left[\beta\left(\eta_{a}(x)-\eta_{b}(x)\right)\right]+\eta_{b}(x)\end{array}$$

즉, Smooth된 Maximum Function에 대입해서 전개해보면

$$\begin{array}{l}S_{\beta}\left(\eta_{a}(x), \eta_{b}(x)\right) =\left(\eta_{a}(x)-\eta_{b}(x)\right) \cdot \sigma\left[\beta\left(\eta_{a}(x)-\eta_{b}(x)\right)\right]+\eta_{b}(x)\end{array}$$

이 될 것입니다!

ACON 안에 Swish 있다 😉

자, 그럼 아까 언급한 Maxout Family에 준하여 여러 Activation을 표현할 수 있었다면, 각각을 Smooth된 Maximum Function에 해당하도록 전개를 해볼까요?

ReLU의 smooth되는 버전이 Swish라는 건 직관으로도 많이들 이해하고 있었는데요. 이 식에서 보듯이 Smooth된 Maximum Function에 대입해서 전개해보면, 바로 Swish 식이 나오게 됩니다. 저자는 이를 통해 Swish가 ReLU의 Smooth Approximation임을 표현할 수 있게 된다고 말합니다.

또한, Leaky ReLU의 상위 호환이기도 한 PReLU(Parametric ReLU, 음수 부분의 기울기 값이 learnable함)도 살펴보면, 역시 Smooth되는 함수로 대응하는 것을 찾을 수 있습니다. (아 이 때 PReLU에 대응하려면, p < 1 인 걸로 한정해서 생각해봐요 우리 🙂)

그리고 마지막으로 각 선형 함수의 가중치(Cartesian 좌표계 상은 기울기겠죠?)가 p1, p2로 표현하면 가장 일반화된 표현일텐데요 (p1 ≠ p2). 여기에 각각 Maxout Family, ACON Family를 대응해보면 일반화된 식이 나옵니다. 위에서 언급한

$$\operatorname{ACON-C}(x):=\left(p_{1}-p_{2}\right) x \cdot \sigma\left(\beta\left(p_{1}-p_{2}\right) x\right)+p_{2} x$$

이 이렇게 유도되게 되는 것이죠!

사실 Maxout Family에서 비교하게 되는 두 함수는 위에서처럼 단순하지 않을 수도 있습니다. 각각이 복잡해질수록 더 많은 함수들을 표현할 수 있게 되죠. 다만, 저자는 이 Maxout Family를 ACON Family로 바꿨을 때(즉, Smooth Maximum Function으로 근사했을 때)의 효과를 보는 데에 연구를 집중했다고 해요. 향후 연구에서 더 전체적인 Scope에서의 비교가 있기를 기대해봅니다!

ACON의 특성

ACON에 특정 값을 대입해서 한번 살펴볼까요?

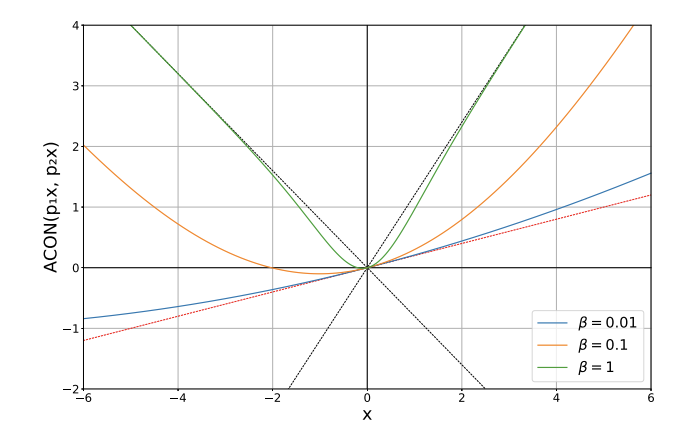
p1=1.2, p2=-0.8일 때 ACON-C에 대응하는 식을 여러 β값에 대해 표현한 graph입니다.

• β가 클 때는, maximum function처럼 반응하여 비선형적인 특성을 갖게 되고요.
• β가 0에 가까울 때는 mean function에 근사되어 선형적인 특성을 갖네요.

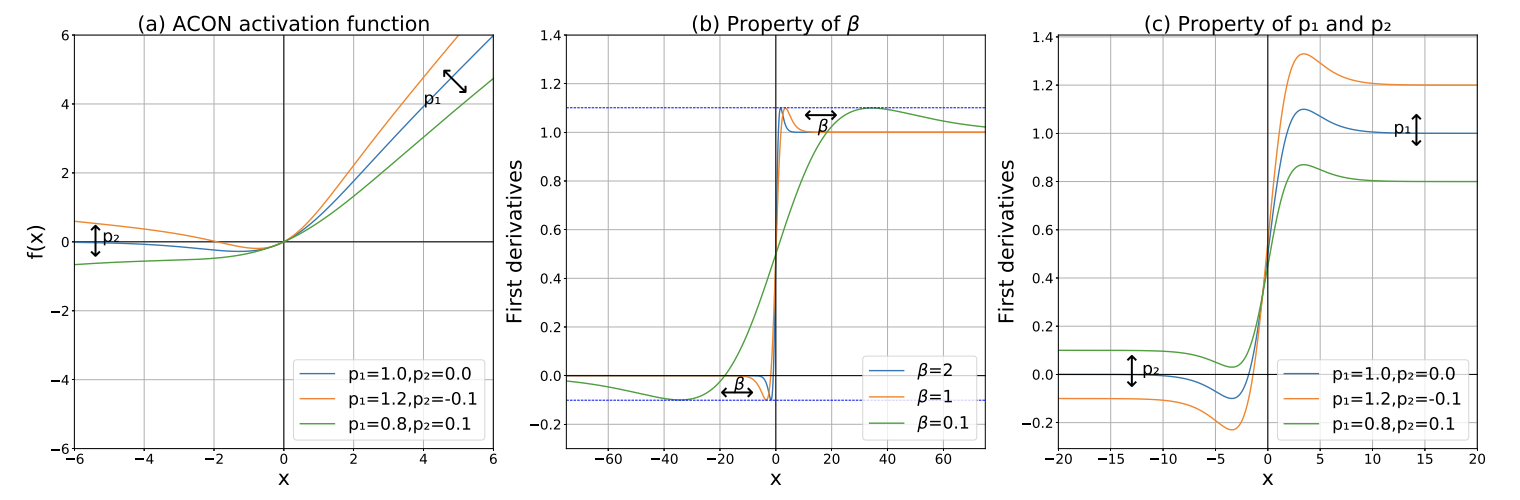
ACON Activation과 이에 대한 도함수(derivative)를 보여주는 그림입니다.

• 왼쪽: β가 fixed 되어 있을 때, p1, p2 계수에 따라 어떻게 Activation function이 달라지는 지를 보여줍니다.
• 가운데: β 값이 달라짐에 따라 ACON의 도함수가 변화하게 되고 이를 통해 β의 역할을 짐작해볼 수 있습니다.
• 오른쪽: β가 fixed 되어 있을 때, p1, p2 계수에 따라 ACON의 도함수가 어떻게 변하는 지를 보여줍니다.

ACON의 도함수를 보면서 아래와 같은 사실을 알 수 있어요.

• p1, p2는 각각 Upper/Lower Bound에 해당하는 값을 결정하게 됩니다.
• β 값은 도함수 상에서 p1, p2에 의해 결정된 Upper/Lower Bound에 얼마나 빠르게 근사되는 지를 결정하게 됩니다.

Swish에서는 Hyperparameter β만이 Upper/Lower Bound에 얼마나 빨리 근사되는 지를 결정하게 되는데요. ACON에서는 p1, p2가 이 Bound 값을 결정하게 되고, 이 역시 learnable해질 수 있다는 특성이 있습니다. 이렇게 boundary가 learnable하다는 것은 optimization을 쉽게 하는 데에 필수적인 특성이고, 저자는 이 장점을 실험 결과를 통해 보여주고 있습니다.

학습에 모두 맡겨버리자! Meta-ACON

Meta-ACON은 β 자체를 Learnable한 parameter로 놔두는 것에서 더 나아가, Layer에 입력되는 feature map으로부터 FC Layers를 거쳐 estimation 되도록 만든 것입니다.

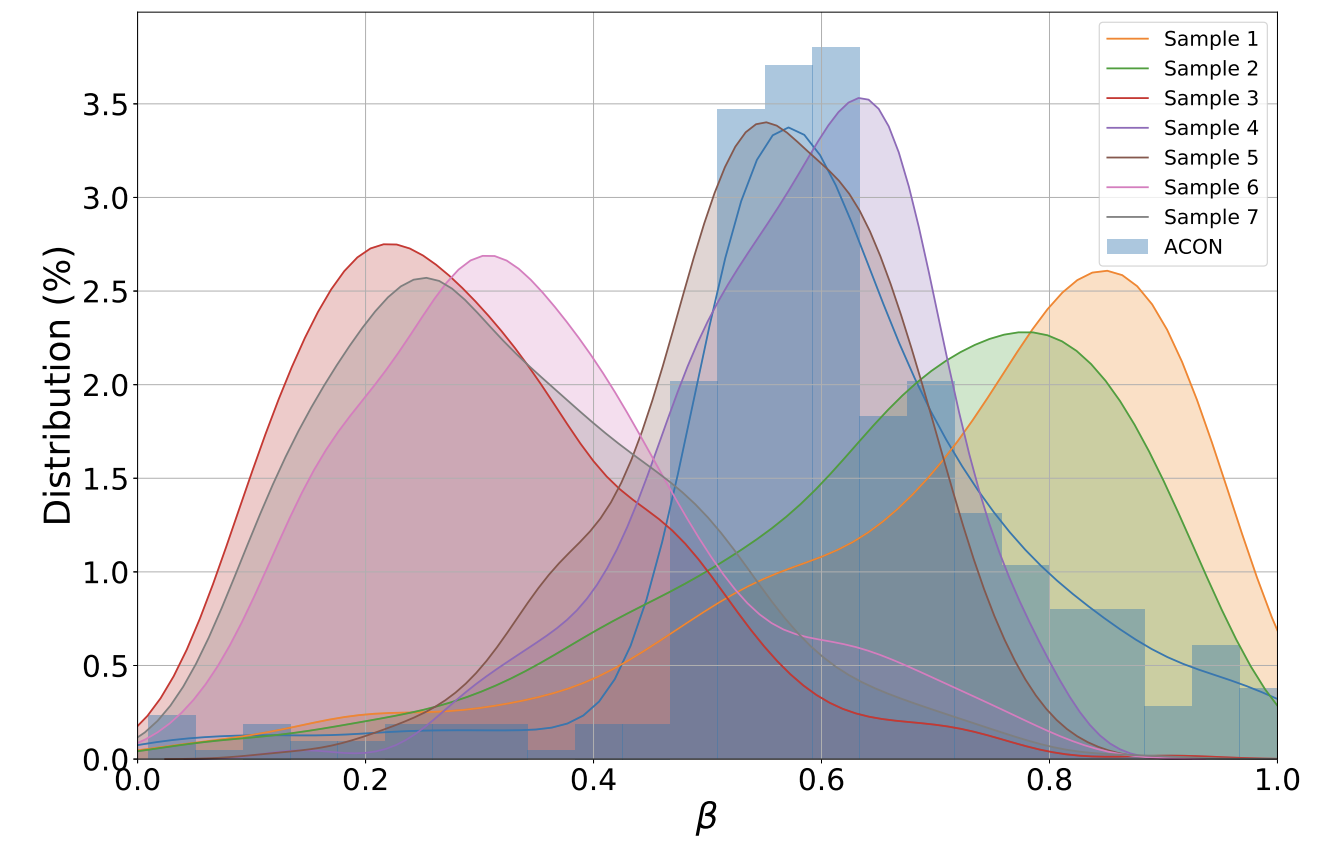
ACON과 meta-ACON을 비교한 도식입니다. ResNet50의 마지막 BottleNeck Layer에서의 activation을 비교한 것입니다. 여기에서 7개의 sample을 임의로 추출해봤습니다.

• ACON에서 추출할 경우, 파란 히스토그램에 해당하는데요. 7개의 sample이 동일한 β distribution을 나타냅니다.
• Meta-ACON에서는 7개의 sample이 서로 다른 β distribution을 보여주게 됩니다. 여기서 β 값이 작을수록, 선형적으로(linear) 반응하는 것이고, β 값이 클 수록 비선형적(non-linear)으로 반응하고 있는 것입니다.

Code Snippet으로 보면 아래와 같습니다. 본 Snippet은 저자의 official github에서 발췌했으며, 해당 Repository에서 자세한 코드를 확인하실 수 있습니다.

결과

ImageNet Classification Result	Accuracy Improvements

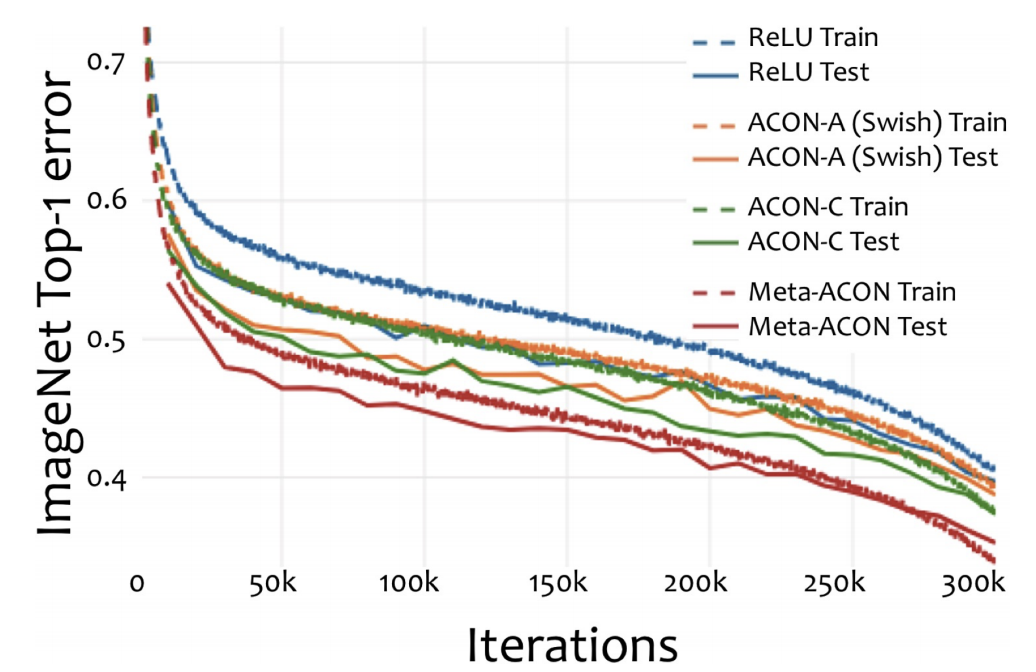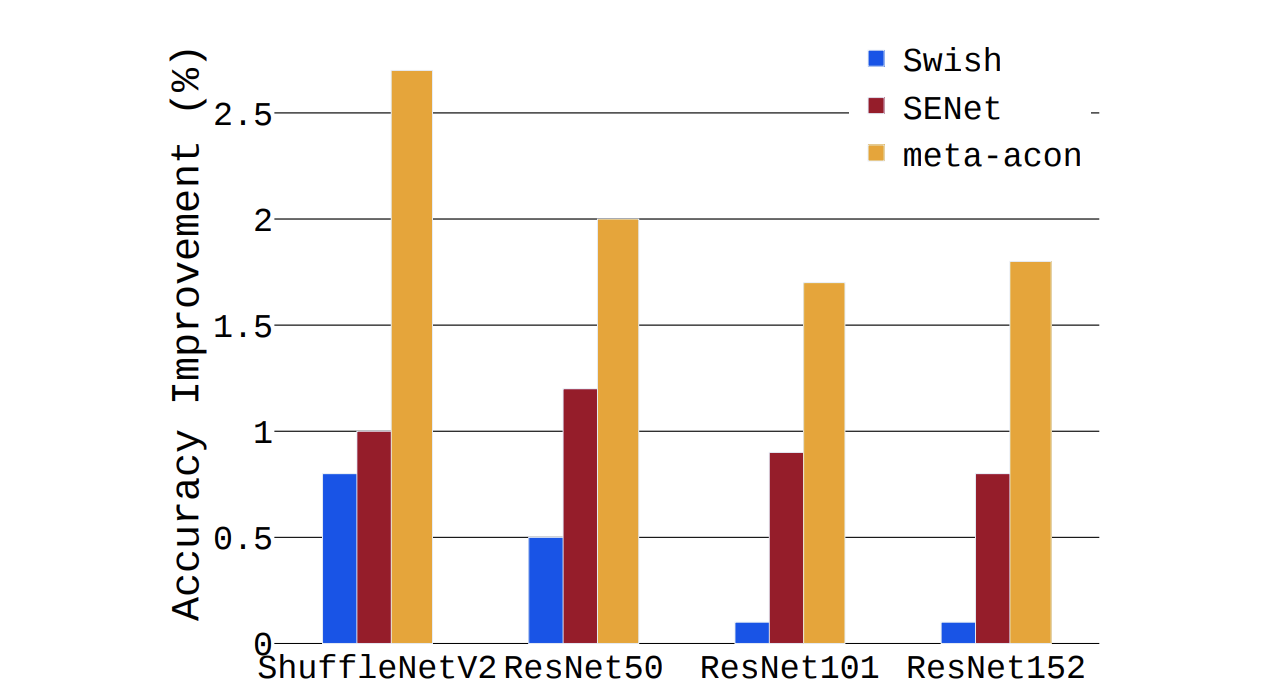ImageNet Classification에 대한 ShuffleNetV2 기준 결과를 살펴보면, 학습 속도도 빠를 뿐더러, Meta-ACON을 사용했을 때 Error rate가 낮아지는 것을 확인할 수 있습니다. 또한, 전반적으로 모델 사이즈가 커질 수록, Meta-ACON을 사용할 수록 Accuracy 향상이 큽니다. (Swish 대체, SENet Novelty 추가 등 대비)

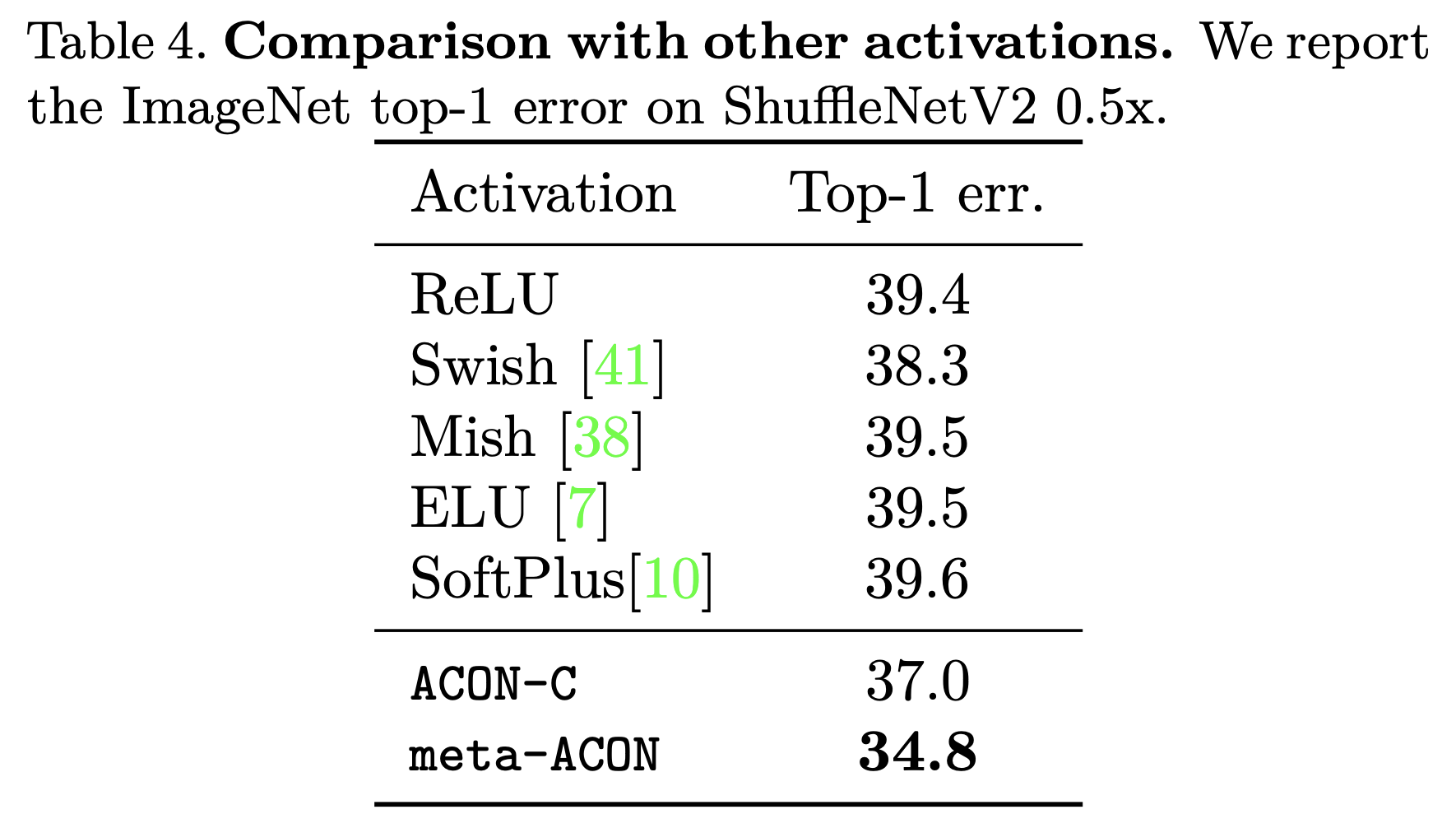
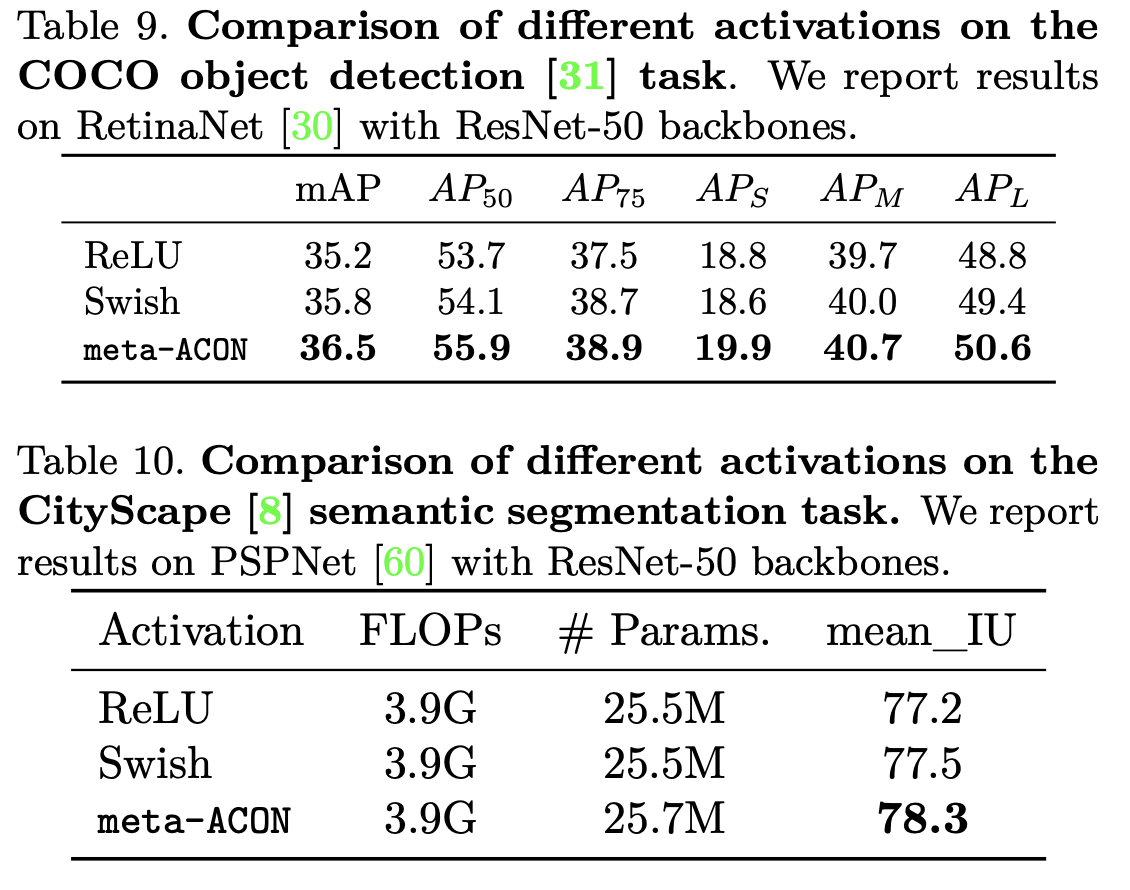
이렇게 Meta-ACON은 다른 activation 대비 ImageNet Classification에서 좋은 성능을 보여주고 있습니다. 또한, 제한적이기는 하나, 특정 backbone에 대해서 Object Detection 및 Semantic Segmentation에 있어서도 다른 activation function을 사용할 때보다 좋은 성능을 보여줍니다.

마무리

이렇게 오늘은 ReLU와 Swish 간의 관계를 통해 새로운 Activation Function들이 포진되어 있을만한 일반화된 식을 찾고(ACON Family), 이를 기반으로 Trainable한 Activation Function을 새로 만나볼 수 있었습니다.
사실 이렇게 훈련 가능한 파라미터를 가진 Activation Function이 ACON만 처음인 것은 아닙니다. 또한, 여러 Sub-task에 대해 범용적으로 사용될 수 있는 Activation Function일지는 미지수이기도 하고요. 특히 모델 경량화 등 어느 한편에서는 Non-linear Activation Function마저 Bottleneck으로 짚고 넘어가는 실정이기에^[3], 모든 목적을 만족시킬만한 새로운 활성 함수를 찾은 연구는 아닙니다. 다만, 식에 대한 간단한 정리로 ReLU와 Swish 간의 관계를 보임과 동시에, 새로운 Activation Family를 제시했다는 데에 의의가 있는 논문이었습니다.

CVPR 2021에서 이러한 논문도 발표된다는 것을 함께 공유하고 싶어 간략하게나마 리뷰를 진행해봤습니다 👍

References (+ 함께 읽으면 좋은 논문들)

1. Ramachandran, Prajit, Barret Zoph, and Quoc V. Le. "Searching for activation functions." arXiv preprint arXiv:1710.05941 (2017). [paper]

2. Goodfellow, Ian, et al. "Maxout networks." International conference on machine learning. PMLR, 2013. [paper]

3. Han Cai, Chuang Gan, Ligeng Zhu, and Song Han. "TinyTL: Reduce Memory, Not Parameters for Efficient On-Device Learning ." Part of Advances in Neural Information Processing Systems 33 (NeurIPS 2020) [paper]

TL;DR

• Activation function들에 대해 기존 Maxout family에 해당하는 일반화를 넘어 ACON Family라는 개념으로 확장하여 일반화를 합니다.
• 이를 통해 ACON Family에서 각 activation을 결정 짓는 parameter 자체를 learnable하게 하여 acon 이라는 activation을 새롭게 제시합니다.
• 기존 Swish 는 NAS로 찾은 activation으로서, 더 좋다는 것만 알 뿐, 왜 좋은지를 몰랐는데, ACON Family에 대응하여 봤을 때, 이를 어느정도 설명할 수 있게 됩니다.